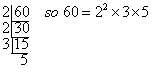
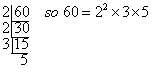
Every composite factor of a number consists of a product of a subset of the prime factors of that number. For each prime factor, think about the number of choices you have. For example, if you were factoring 60=2²×3×5, there would be
3 choices for the number of 2's: 0, 1, or 2,
2 choices for the number of 3's: 0 or 1, and
2 choices for the number of 5's: 0 or 1,
for a total of 3×2×2 = 12 choices.
We have
2⁰ × 3⁰ × 5⁰ =   1,       2⁰ × 3⁰ × 5¹ =    5,
2¹ × 3⁰ × 5⁰ =   2,       2⁰ × 3⁰ × 5¹ =  10,
2² × 3⁰ × 5⁰ =   4,       2⁰ × 3⁰ × 5¹ =  20,
2⁰ × 3¹ × 5⁰ =   3,       2⁰ × 3⁰ × 5¹ =  15,
2¹ × 3¹ × 5⁰ =   6,       2⁰ × 3⁰ × 5¹ =  30,
2² × 3¹ × 5⁰ = 12,      2⁰ × 3⁰ × 5¹ =  60